Transport optimal et flots de gradient, un nouveau regard sur (une partie de) la physique
Bertrand MAURY
Université Paris-Saclay
Formulé par Monge à la fin du XVIIIe siècle, le problème du transport optimal de masse a été « dormant » pendant plus dun siècle, il a suscité un regain dintérêt au milieu du XXe siècle suite aux travaux fondateurs de Kantorovich en URSS, et a connu un troisième essor, fulgurant, il y a une trentaine dannées, il sagit maintenant dun domaine à part entière de lanalyse mathématique et du calcul des variations. Nous souhaitons présenter comment cette approche, qui vise au départ à estimer le coût de transport dune distribution de masse donnée vers une zone daccueil de cette masse, permet de définir une distance sur lespace des mesures de probabilité (ou plus généralement des mesures positives dune masse totale donnée). Il est alors possible de définir sur ce nouvel espace métrique des notions a priori réservées aux espaces euclidiens ou hilbertiens, comme la notion de flot de gradient (mouvement suivant la ligne de plus grande pente dune fonction de « paysage » donnée). Cette approche jette une nouvelle lumière sur des équations hyperclassiques, comme léquation de la chaleur, qui peut être vue dans ce contexte comme un flot de gradient pour la fonctionnelle dentropie. Nous présenterons des extensions plus exotiques de cette approche, en particulier dans le domaine du mouvement de cellules ou de foules, ou de certains modèle fluides (écoulements de Hele-Shaw ou équations dEuler sans pression avec contrainte de congestion).
IMAGES
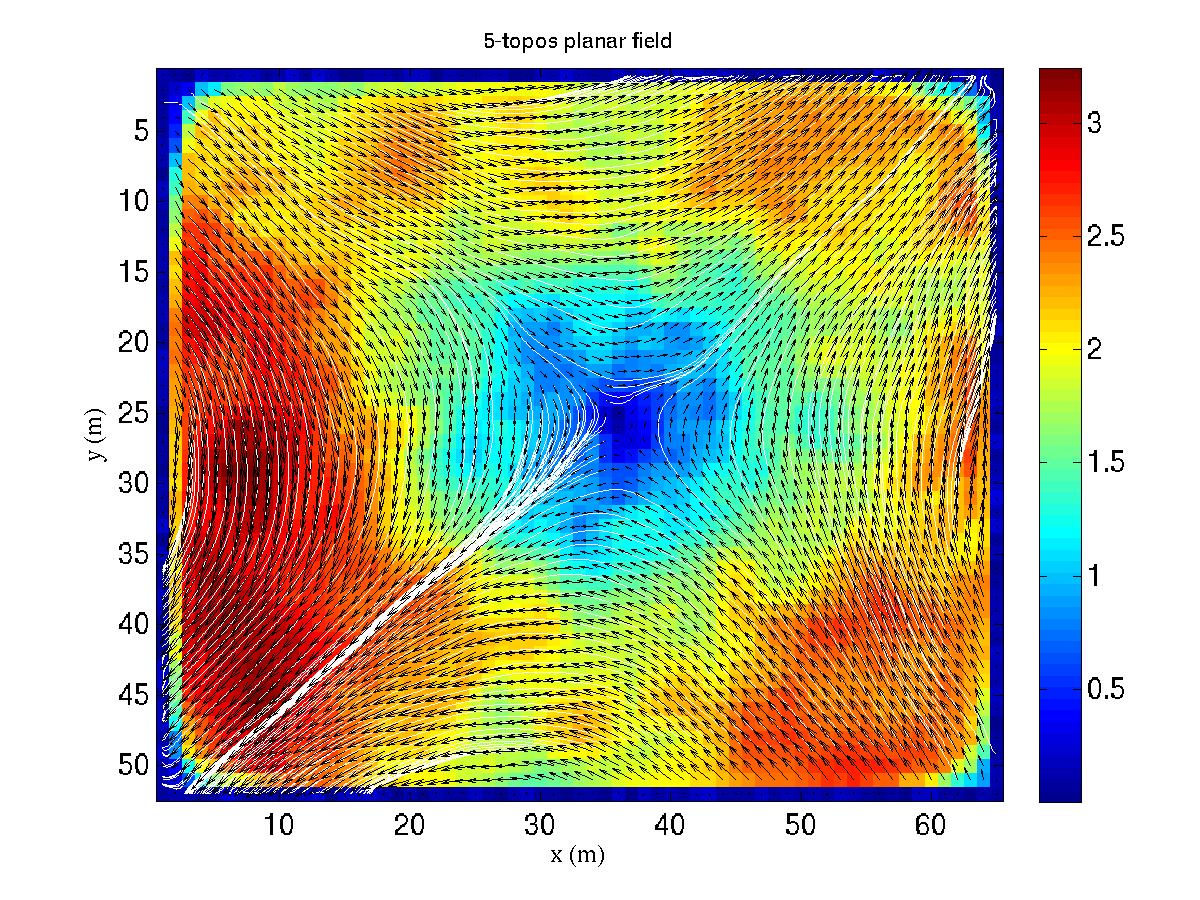
Ecoulement en micro-canal (plus de détails...)
CONFÉRENCES
2nd European Fluid Dynamics Conference, Dublin, Ireland, 26 Août 2025