Nonlinear forward-backward parabolic equations
Anne-Laure DALIBARD
Laboratoire Jacques-Louis Lions, Sorbonne Université
Résumé :
Cet exposé sera consacré à létude des solutions de léquation
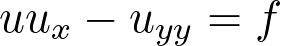
dans un domaine 2d, qui est vue comme un « modèle-jouet » pour léquation de Prandtl stationnaire. Le but est de construire des solutions changeant de signe (et donc comportant une bulle de recirculation), au voisinage de profils explicites, en perturbant le terme source et/ou les données au bord. Cette équation peut être vue comme une équation parabolique (de type « chaleur » ) dans le sens direct (forward) dans la zone où u est positive, et dans le sens rétrograde (backward) dans la zone où u est négative, ces deux zones étant séparées par la ligne où u = 0, qui est une frontière libre.
On sattendrait à ce que pour des données régulières (cest-à-dire pour un terme source et des données au bord régulières), on puisse construire une solution régulière. Or, on peut montrer que ça nest pas le cas : génériquement, même pour des données très régulières, les solutions possèdent des singularités au voisinage des points dannulation de u sur les bords latéraux. La solution est régulière si et seulement si les données vérifient certaines conditions dorthogonalité. Ce phénomène est déjà présent pour des variantes linéaires de léquation ci-dessus, mais perdure dans le cas non linéaire.
Dans cet exposé, jexpliquerai la nécessité des conditions dorthogonalité, et je présenterai les profils singuliers associés à léquation. Je donnerai également quelques éléments sur la construction des solutions lorsque les conditions dorthogonalité sont vérifiées.
Il sagit dun travail en commun avec Frédéric Marbach et Jean Rax.
Abstract:
This talk will be devoted to the study of solutions of the 2d equation
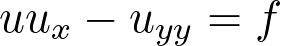
which acts as a "toy model" for the stationary Prandtl equation. The goal is to construct solutions that change sign (and thus include a recirculation bubble), in the neighborhood of explicit profiles, by perturbing the source term and/or the data on the boundary. This equation can be seen as a parabolic (heat-like) forward equation in the area where u is positive, and as a backward equation in the area where u is negative. These two areas are separated by the line where u = 0, which is a free boundary.
One would expect that for regular data (i.e. for regular source term and boundary conditions), one could construct a regular solution. However, it can be shown that this is not the case: generically, even for very regular data, the solutions have singularities in the neighborhood of the cancellation points of u on the lateral edges. The solution is regular if and only if the data verify some orthogonality conditions. This phenomenon is already present for linear variants of the above equation, but persists in the nonlinear case.
In this talk, I will explain the necessity of the orthogonality conditions, and I will present the singular profiles associated with the equation. I will also give some elements on the construction of solutions when the orthogonality conditions are verified.
This is a joint work with Frédéric Marbach and Jean Rax.
IMAGES
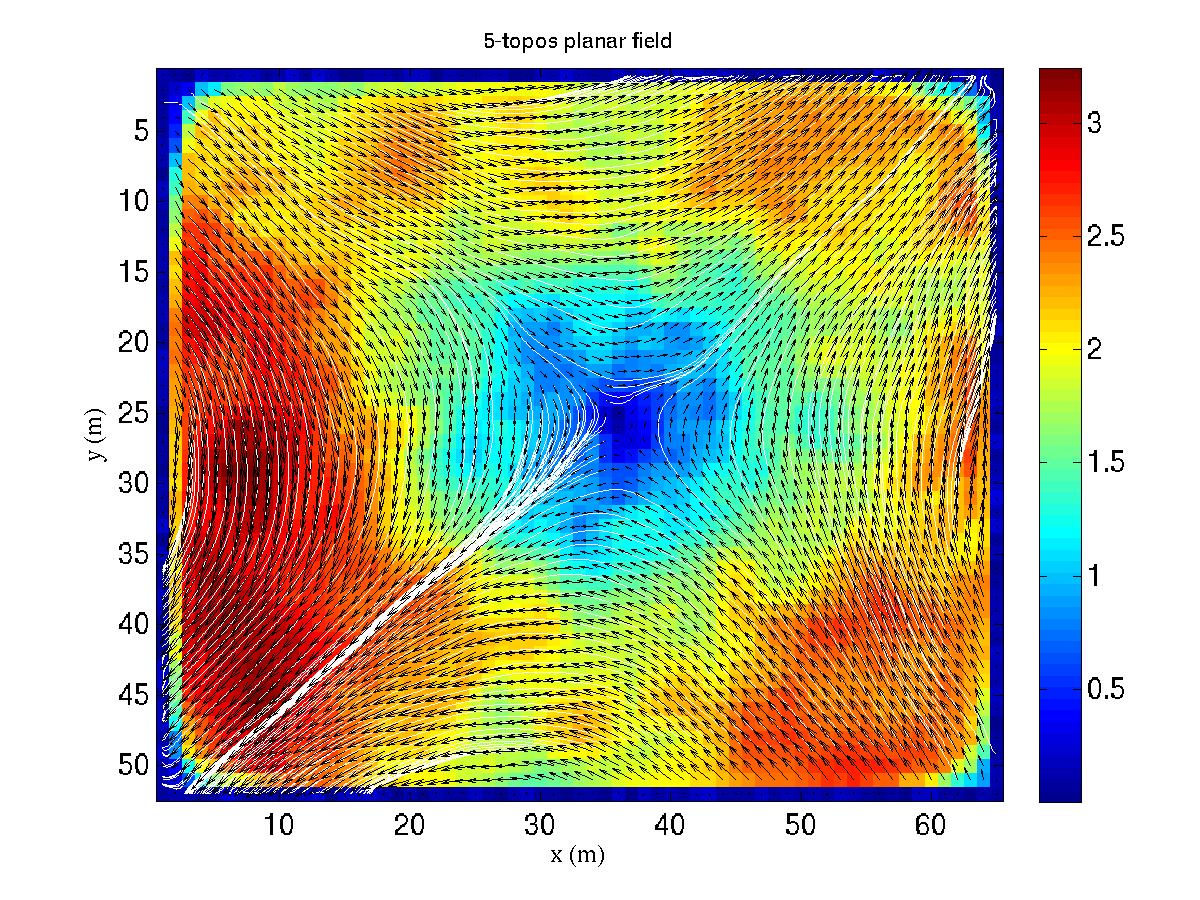
Ecoulement en micro-canal (plus de détails...)
CONFÉRENCES
2nd European Fluid Dynamics Conference, Dublin, Ireland, 26 Août 2025