Pourquoi une communauté du Non-Linéaire ?
"....la physique ne nous donne pas seulement l'occasion de résoudre
des problèmes; elle nous aide à en trouver les moyens, et cela de deux manières.
Elle nous fait pressentir la solution; elle nous suggère des raisonnements."
POINCARÉ, Valeur sc., 1905, p.152.
Comme il est souvent le cas dans les autres disciplines, l'évolution
de la science du non-linéaire a procédé par paliers,
avec des aller-retours entre développement des méthodes
et techniques mathématiques et application à des phénomènes
réels. Mais plus que d'autres peut-être, cette
science dépend très étroitement des mathématiques
appliquées. Au XIXème siècle, il s'agissait
pour les mathématiciens de résoudre des équations
différentielles non-linéaires, l'exemple-type étant
fourni par la mécanique céleste. Cependant, dès la
moitié du siècle, les problèmes non-linéaires
s'étudiaient au cas par cas sans concept général,
comme par exemple pour les ondes non-linéaires (Stokes 1847, Riemann
1858).
Avec H. Poincaré qui
établit les bases unificatrices pour l'étude des problèmes
de la mécanique non-linéaire[1,2], et Liapounov qui
pose le problème général de la stabilité [3],
les outils mathématiques nouveaux apparaissent. Suit une période
de sommeil relatif.
En même temps,
dans notre enseignement, l'idée dominante en cours au début
du XX ème siècle, malgré Stokes, Riemann, Poincaré
et autres, est : "Les problèmes de
la Physique mathématique dépendent en général
d'équations aux dérivées partielles d'ordre supérieur
au premier, mais linéaires par rapport à la fonction
inconnue et à ses dérivées." (Jordan : Cours
d'Analyse de l'Ecole Polytechnique 1908-1909, page 244).
Dans les années
1927-1938, l'école russe surtout (Mandelstam-Andronov) commence
à appliquer ces méthodes à des modèles en relation
avec des problèmes pratiques en mécanique des vibrations
de structures, en électricité (oscillateurs), et en optique
(diffraction). Par ailleurs, d'autres écoles se développent
et les applications sont même étendues en science du
vivant (rythmes cardiaques : Van der pol et Van der Mark 1928 [4];
dynamique des populations : Volterra 1931 [5]).
Dans certains pays
ces méthodes sont introduites dans l'enseignement et par exemple,
dans son "Introduction to Non-Linear Mechanics ", un cours sur des applications
pour les ingénieurs de la marine, N. Minorsky note en 1944:
" This report
aims to bring to the attention of technical personnel, both of the Navy
and of other agencies engaged in the war effort, certain new developments
in applied mathematical methods. These new methods have come to be
called "Non-Linear Mechanics"..... Practically all differential equations
of Mechanics and Physics are non-linear...". En d'autres
termes, la Physique (représentation du monde réel) est
d'abord non-linéaire.
Il apparait donc déjà
que la solution à certains problèmes concrets passe par l'étude
complète des modèles non-linéaires : "...Thus,
it became necessary to attack the non-linear problems directly instead
of evading them by dropping the non-linear terms.."
Dans les années
1960-80 les outils mathématiques sont encore développés
("systèmes dynamiques") et les applications deviennent très
nombreuses en hydrodynamique, optique, mécanique, matière
condensée, métallurgie et même en sociologie, économie
etc... L'école fran\c caise de mécanique non-linéaire
qui avait été une des plus actives dans les années
30 (Denjoy, ...) réapparaît et la communauté
est actuellement une des plus nombreuses au monde (signalons que c'est
sans doute l'article de Ruelle-Takens de 1972 qui a relancé l'intérêt
des physiciens).
Actuellement, le message
de Minorsky est toujours d'actualité et pourtant les méthodes
et concepts de la Physique non-linéaire diffusent lentement dans
pratiquement tous les domaines. La physique non-linéaire est
à la fois un domaine fondamental de la science et un thème
unificateur largement interdisciplinaire. Elle doit faire partie du bagage
de tout étudiant en physique, mathématique, mécanique,
chimie, au même titre que le calcul différentiel, la cinématique
du point, ou la mécanique quantique. La mission de l'Université
qui est de préparer les étudiants à l'évolution
de la science, doit inclure l'enseignement des méthodes non-linéaires.
Or, ces méthodes
sont appliquées depuis longtemps. En 1985 la NASA utilise les propriétés
de sensibilité aux conditions initiales du "problème à
trois corps" pour re-diriger avec très peu d'énergie une
sonde (ISEE-3/ICE) vers une comète. Très récemment
(juin 1999) le CNET a porté le débit d'informations dans
une fibre optique à 1012 bits/s en utilisant des solitons
pour support.
Il est alors surprenant
que notre Université, peut-être encore sous l'effet des affirmations
péremptoires de Jordan (1908), et cinquante ans après Minorsky,
tarde à introduire les bases de cet enseignement.
Comme pour d'autres
disciplines, la multiplication des domaines d'application favorise la dispersion
et le cloisonnement. Aussi il est nécessaire d'opérer
à certain moment un rassemblement des thèmes pour permettre
une progression des études théoriques ou des méthodes
expérimentales, par la comparaison et l'échange.
C'est un des objectifs
des "Rencontres du Non-linéaire". Leur succès montre
qu'il existe en France aussi, une communauté très active
et nombreuse en Physique non-linéaire. Le caractère
interdisciplinaire des rencontres doit permettre un échange des
idées mais aussi des personnes. L'accent est mis sur la participation
aux exposés, des doctorants en fin de thèse et ces rencontres
annuelles devraient favoriser la migration des jeunes chercheurs vers des
équipes ou des thèmes différents. Certains pourraient
aussi, par ce biais, découvrir les aspects industriels nouveaux
et des voies professionnelles différentes dans lesquelles s'engager.
Afin de faciliter la transmission des informations
et l'organisation de la communauté du non-linéaire, un serveur
destiné à la Physique Non-Linéaire est en place (http://pnl.lps.u-psud.fr/pnl/).
Il est recommandé de l'utiliser et de lui fournir des informations
à diffuser, dans l'intérêt de tous.
Nous tenons à remercier J.
Oesterlé, Directeur de l'IHP, et E. Guyon Directeur de l'ENS
pour leur aide à l'organisation de ces Rencontres.
P. Collet, P. Coullet, P. Glorieux, Y. Pomeau, R. Ribotta, J-C. Saut, B. Schmitt
[1] "Sur les courbes définies par une équation différentielle"
H. Poincaré, Oeuvres, Gauthier-Villars, Paris, Vol. 1, (1928).
[2] "Les méthodes nouvelles de la mécanique céleste"
H. Poincaré, Gauthier-Villars, Paris, Vol. 1, (1892).
[3] "Problème général de la stabilité du
mouvement" M.A. Liapounoff, Annales de la Faculté des sciences de
Toulouse, Paris Vol. 9, 1907.
[4] "Leçons sur la théorie mathématique de la
lutte pour la vie" , V. Volterra, Gauthier-Villars, Paris, (1931).
[5] "Le battement de coeur considéré comme oscillation
de relaxation" , B. Van der Pol et Van der Mark, Onde Electrique, Paris,
p. 365 (1928).
IMAGES
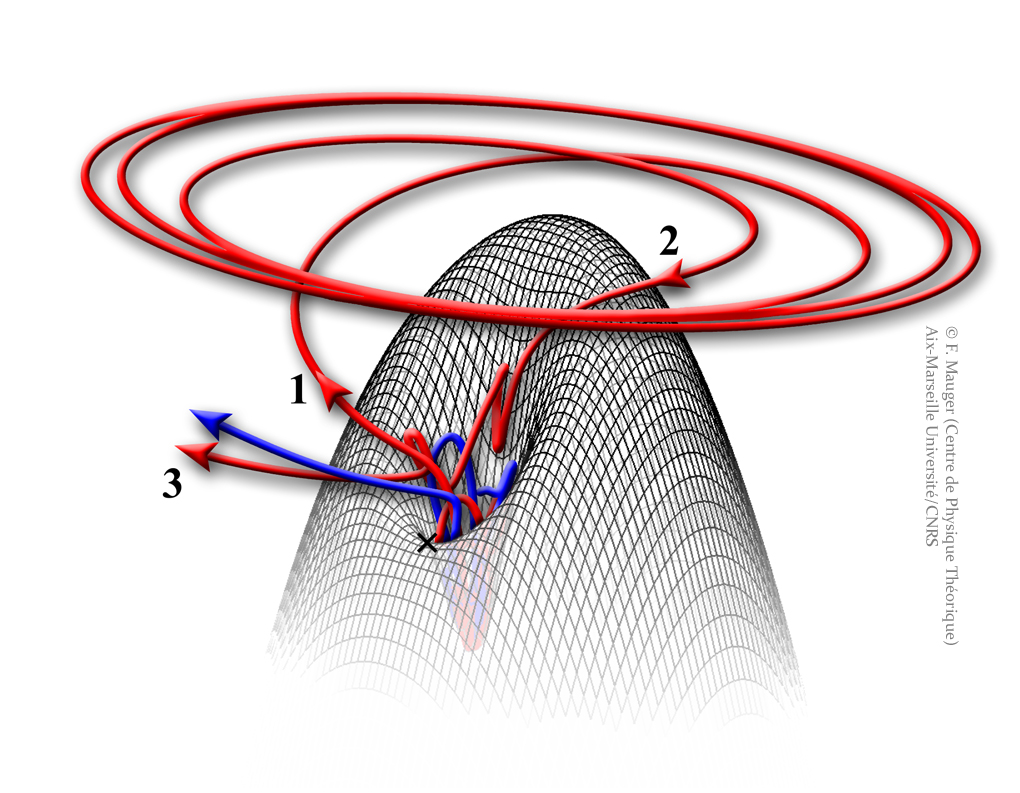
Recollision entre électrons en polarisation circulaire (plus de détails...)
CONFÉRENCES
2nd European Fluid Dynamics Conference, Dublin, Ireland, 26 Août 2025