Images du non linéaire
Vous avez la possibilité de proposer une image illustrant un des thèmes du non linéaire, au sens large, afin qu'elle soit incluse dans cette collection. Elle sera mise en ligne après avoir été visée par le comité éditorial. Il est entendu qu'une image ne sera soumise qu'avec l'autorisation explicite des auteurs. [Soumettre une image]Si vous voulez agrandir une image, ou lire l'intégralité d'une description tronquée, cliquez sur l'image.
Régimes dynamiques de l'injection optique Pascal Besnard, Stéphane Blin, Olivier Vaudel
Soumis le 6 Jan 2007 par Pascal BESNARD
Mot(s)-clé(s) : laser, injection optique, non linéaire, chaos
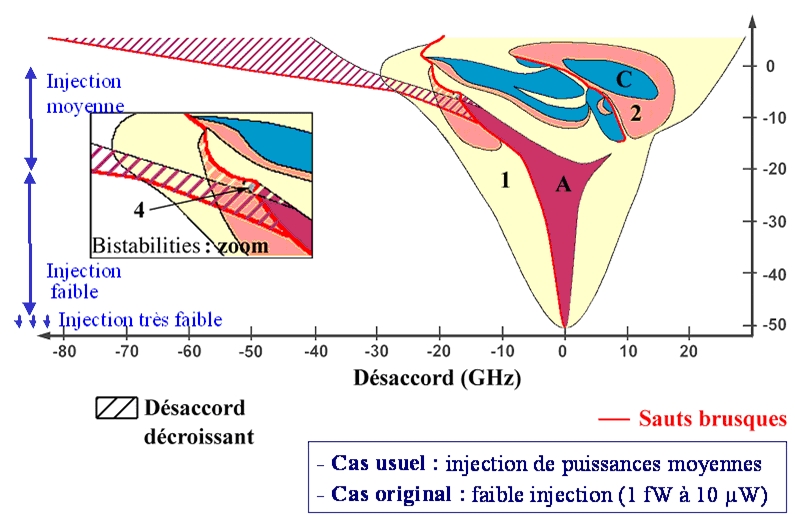
Cartographie expérimentale des comportements dun laser injecté en fonction du désaccord croissant ou décroissant et de la puissance injectée. Le désaccord correspond à la différence de fréquence entre le laser maitre et le laser esclave. Les différentes couleurs correspondent à des régimes de fonctionnement dun laser injecté (A pour accrochage en fréquence ; la zone 1 correspond à un régime non linéaire appelé régime multi-ondes où lon observe des mélanges dondes qui correspondent schématiquement à des battements ; la zone 2 correspond à ce quon appelle du doublement de période (la période est multipliée par rapport à un régime de ...
Organisation topologique d'un attracteur spirale M. Lefranc (PhLAM/CNRS)
Soumis le 5 Jan 2007 par Marc LEFRANC
Mot(s)-clé(s) : chaos, topologie, orbites périodiques instables
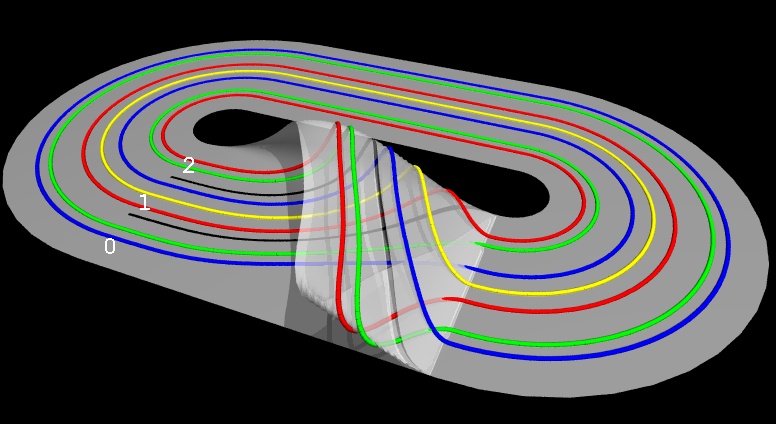
Cette surface bi-dimensionnelle à plusieurs branches (un gabarit, ou template en anglais) décrit de manière concise l'organisation topologique globale d'un attracteur "spirale", ou "entonnoir" ("funnel"), tel qu'on peut en observer dans le système de Rössler pour certaines valeurs des paramètres. En particulier, toutes les orbites périodiques instables de l'attracteur peuvent être projetées sur cette surface sans modifier leurs types de noeud ni leurs invariants topologiques. Sont ainsi représentées ici une orbite de période 1, en jaune, et trois orbites de période 2, en bleu, vert, rouge. Les quelques invariants décrivant la structure de cette surface fournissent des signatures des processus ...
Étirement et repliement M. Lefranc (PhLAM/CNRS)
Soumis le 5 Jan 2007 par Marc LEFRANC
Mot(s)-clé(s) : chaos, attracteur, section de Poincaré, étirement, repliement
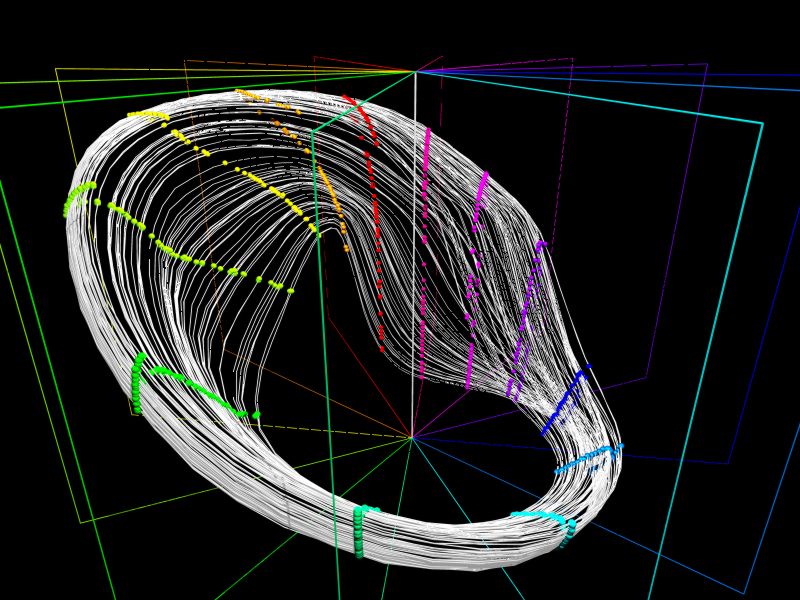
L'attracteur associé à un régime chaotique observé dans un laser C02 à pertes modulées est représenté ici dans un espace des phases reconstruit à l'aide de coordonnées décalées dans le temps. En suivant (dans le sens trigonométrique) les intersections successives de l'attracteur avec une série de sections de Poincaré (indiquées en couleur), on visualise les mécanismes géométriques d'étirement et de repliement qui façonnent l'attracteur chaotique.
IMAGES
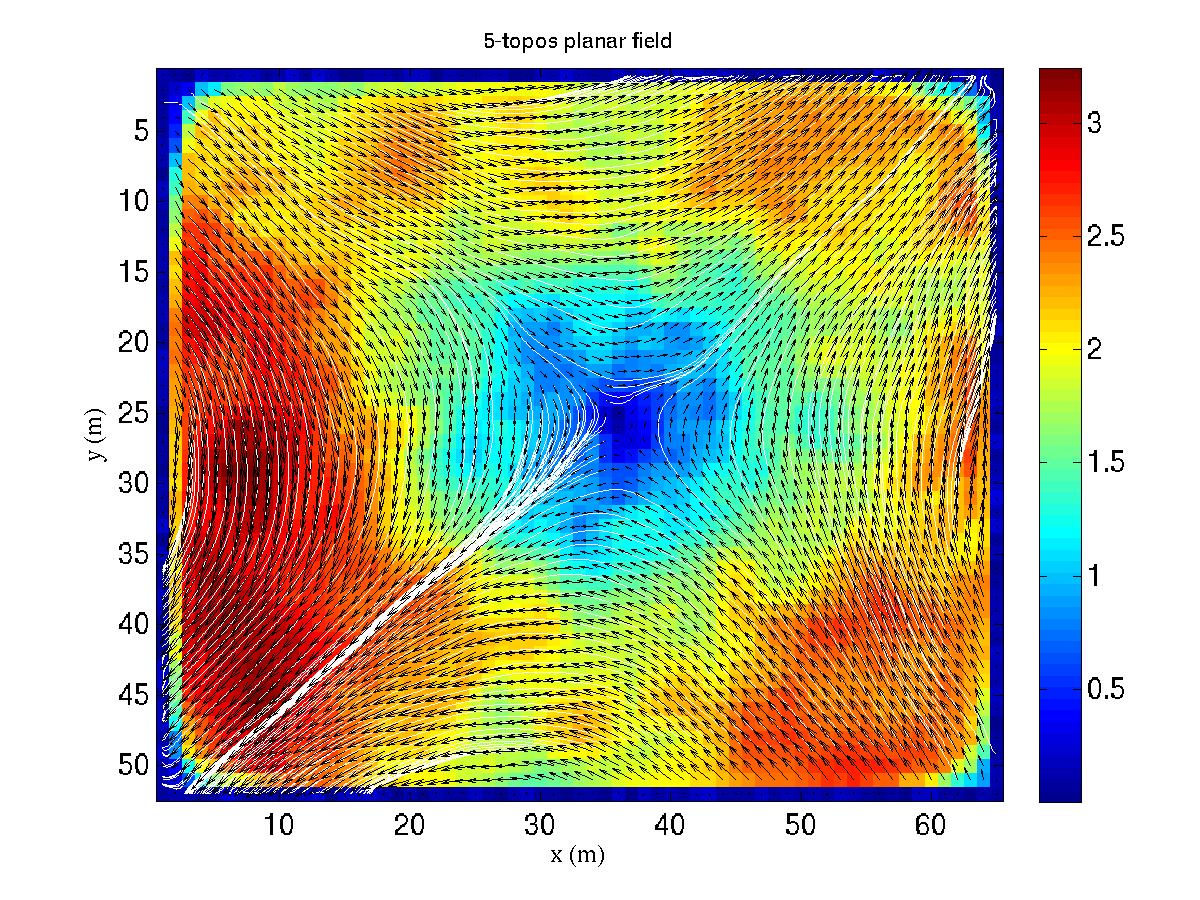
Ecoulement en micro-canal (plus de détails...)
CONFÉRENCES
2nd European Fluid Dynamics Conference, Dublin, Ireland, 26 Août 2025